Interpreters
So whats an interpreter?
A program that accepts statements, executes them immediately and then outputs the result.
At it's core these are the only 3 things an interpreter does

- Accepts input
- Executes statement inputted
- Outputs result
An interpreter needs to loop through these three steps over and over to allow for more and more input (the Python interpreter doesn't stop after typing one thing). We call this the Read-Eval-Print-Loop (REPL)
Note: an interpreter is likely to be implemented in a different language than which it interprets (example: scheme interpreter written in python)
REPL
Each part of this loop can be further divided up:
Read:This is the part where the interpreter accepts an inputLexer:Turns strings into list of 'tokens', small important piecesParser:Takes the 'tokens' and puts it into a format to make the job of the interpreter easier
Eval:This is the part where the interpreter does stuff with what was inputtedEval:takes expressions and evaluates them according to specification of the language (may callapplyto figure out what it may eval to)Apply:applies a function to the operands (may callevalto figure things out)
Print:This is where the interpreter displays the results to the user
Pictorally:
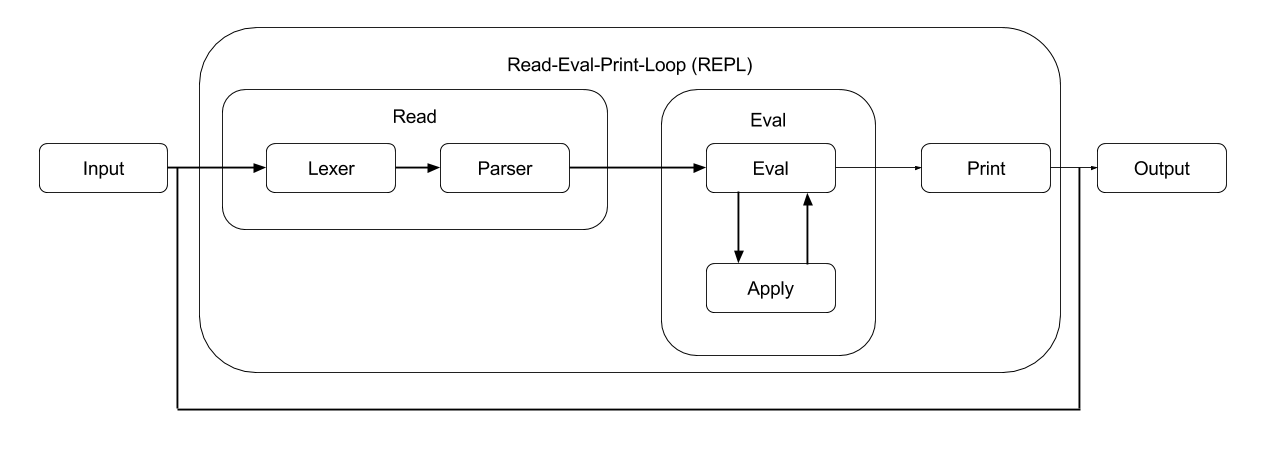
Read
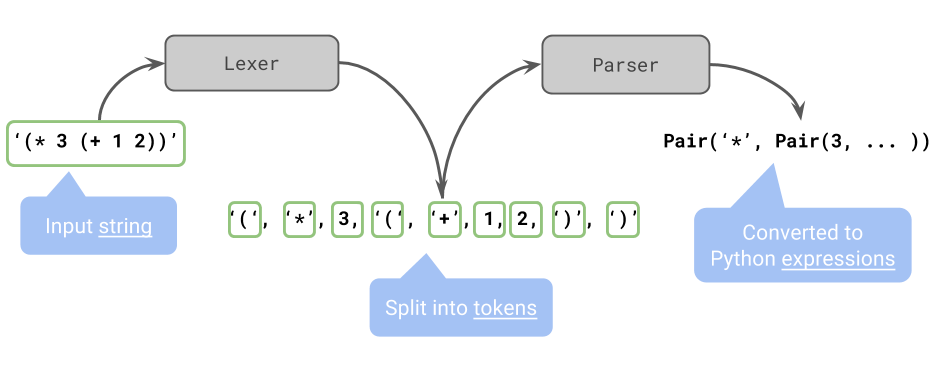
This is an example of the lexer/parser from the scheme project (pulled from lec 21):
Eval/Apply
Follow the same steps as usual for call expression!
- Evaluate operator
- Evaluate operand(s)
- Apply operator to operand(s)
Apply
When we apply a function we follow the process we followed before when constructing environment diagrams:
- Create a new frame
- Assign parameters to values
- Evaluate the body of the function
| Eval | Apply | |
|---|---|---|
| Base Cases: | Primitive values | Built-in primitive procedures |
| Symbols | ||
| Recursive Calls: | eval(sub_expression) for special forms | eval(body) of user-defined procedure |
| eval(operator, operands) for call expressions | ||
| apply(procedure, arguments) |
Counting Calls
This is the process of determining the number of calls to eval and apply are needed to fully evaluate a statement.
You'll want to use the process for evaluating call expressions to determine the number of eval/apply calls.
For example:
xxxxxxxxxx(+ 1 2)To determine the number of calls let's walk through the statement element by element:
(+ 1 2)this is what we were inputted and we have to call eval on it to do anything with it (+1 eval)now we follow the 3 previously mentioned steps
+here we evaluate the operator (+1 eval)- 1 we evaluate an operand (+1 eval)
2we evaluate an operand (+1 eval)- apply
+to1and2, this is the final step for call expressions (+1 apply)
In this case we had: 4 evals and 1 apply
Problems
What does lexer turn these into?
(1 2 4)(define (f x) 5)
What does the parser turn these into?
xxxxxxxxxx['(', '+', 1, 2, ')']xxxxxxxxxx['(', 1, '(', 2, ')', 3, ')']
How many calls to scheme_eval/scheme_apply?
xxxxxxxxxx(define (f x) (* ((lambda () x)) 2))xxxxxxxxxx((lambda (x y) (+ (y 2) x)) 3 f)xxxxxxxxxx(let ((f 4)(g f))(g (+ f (eval (define h ((lambda (a b) (* a b)) f 5))))))xxxxxxxxxx(+ (* (if (and #t) 1 2) 4) (begin (+ 1 2) (+ 3 4)))
Generalized counting Eval/Apply
Given these general forms, write the number of Eval/Apply calls in terms of the expressions (for these problems assume these can be anything so we'll generalize by using and ):
Example:
xxxxxxxxxx(/ a b)Solution:
Evals (total of )
- , for total evaling entire statement
(/ a b)and evaling/ - represents the number of evals for
aandbcombined
- , for total evaling entire statement
Apply (total of )
- 1, for applying
/toaandb - representing the number of applies to evaluate
aandb
- 1, for applying
xxxxxxxxxx(define a (+ b c))xxxxxxxxxx(if a b c)xxxxxxxxxx(define (fn a b) c)xxxxxxxxxx(let ((a b) (c d)) e)xxxxxxxxxx((lambda (a) b) c)xxxxxxxxxx(and a b c)- AخA
(begin a b c)